Simon Lautenbach
muphyII plasma simulation framework
The muphyII code is a simulation framework for collisionless plasma physics and targeted at space plasmas in particular. The muphyII code utilizes a hierarchy of models with different inherent scales to address the separation of scales problem typically encountered in these plasmas. It allows stand-alone use of models as well as a model-based dynamic and adaptive domain decomposition and resorts to novel techniques for energy conservation, careful treatment of inner-domain model boundaries for interface coupling, and robust time stepping algorithms.
| Current code version | 1.0 |
| code/repository | Zenodo, GitHub |
| Legal Code License | MPL-2.0 |
| Software code languages and tools | C++, Fortran, MPI, OpenACC |
coupling animations from muphyII simulations
Motivation
The separation of spatial and temporal scales generally encountered in plasmas can span up to nine orders of magnitude or more, which makes the accurate treatment of plasma behavior a huge challenge for numeric simulations. It is impossible (and remains so for the foreseeable future) to perform plasma simulations on the finest level of physical description, the kinetic scales, while accounting for dynamics on all other scales up to system size as well. Conversely, it is impossible to simulate the whole system, say the solar wind or Earth’s magnetosphere, and resolve all scales that contribute to and often substantially alter plasma dynamics. Kinetic models need to be localized to small regions of most interest to treat large-scale phenomena numerically. Fluid models can provide an approximation of kinetic physics but lack some important kinetic effects. However, they are inherently cheap (compared to kinetic models) and neglect fine-scale processes outside the fluid description, thus allowing treatment on coarser scales. Within the class of fluid models, several descriptions of different fidelity can be derived as specific reductions from the kinetic equation.
The collisionless plasma physics solver of the muphyII framework uses a multiphysics approach to address the separation of scales. Firstly, we draw on a hierarchy of models, ranging from fully kinetic Vlasov simulations to hybrid Vlasov/10-moment-Fluid, to fully 10-moment-Fluid, to hybrid 10/5-moment fluid, to fully 5-moment fluid model figure . Each model down the hierarchy provides a coarsening of relevant scales and a severe reduction in computational cost but also reduces physical fidelity and expressiveness. In the context of muphyII, hybrid refers to models that treat ions and electrons differently. Note that hydrogen ions (i.e. protons) and electrons are usually the two dominant particle species present in most plasmas and, in particular, those targeted by the muphyII plasma solver, namely collisionless, non-relativistic, non-degenerate space plasma.
 Hierarchy of available models.
Hierarchy of available models.
Secondly, we can adaptively and dynamically couple these models based on the desired fidelity in each subregion of the simulation domain [1]. This concept exploits the observation that many large-scale phenomena like magnetic reconnection or collisionless shocks display a separation of regimes that reduce the need for high-fidelity modeling to very localized regions in space. An idealistic sketch of the approach is depicted in figure .
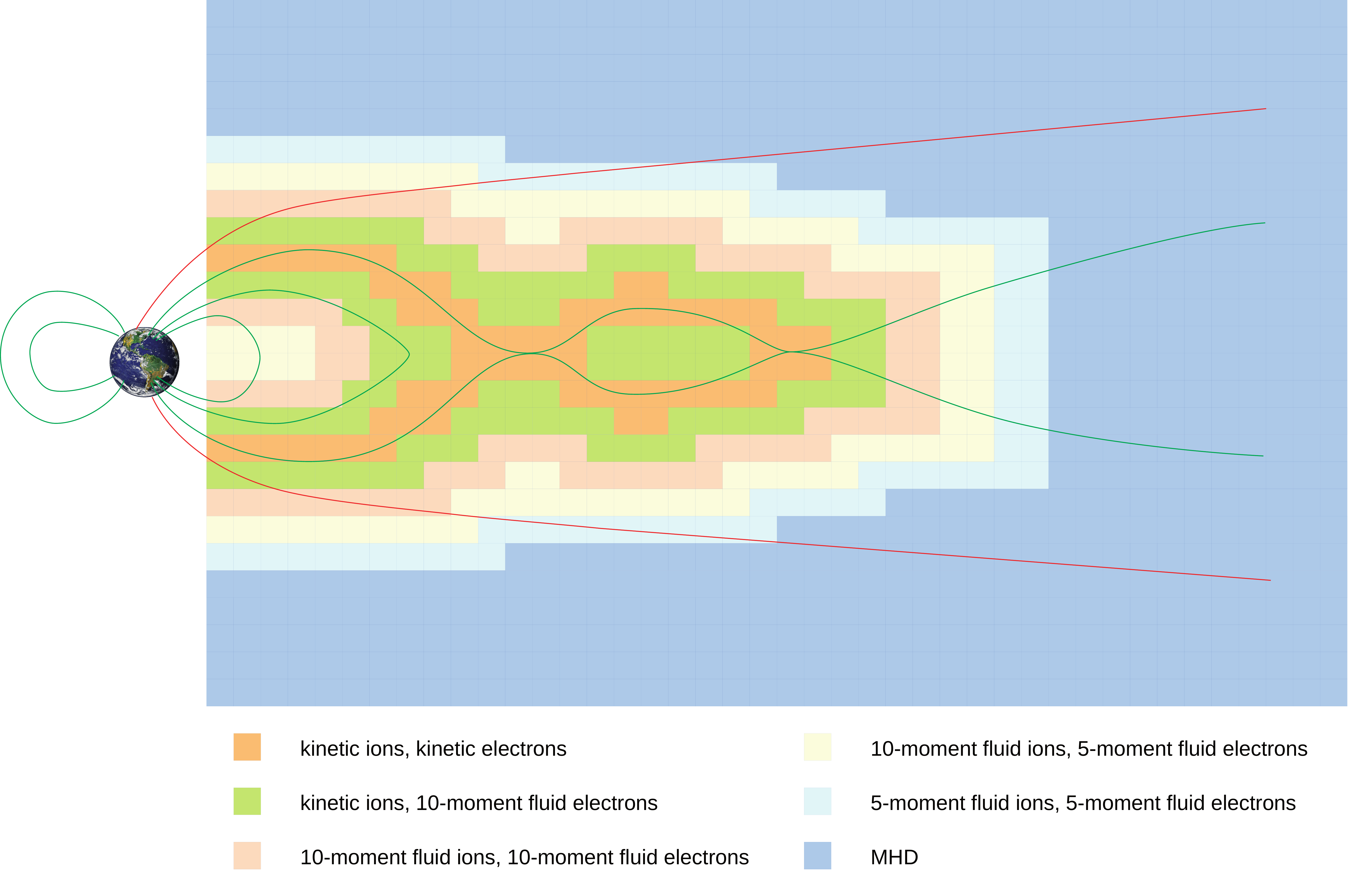 Oversimplified sketch of a multiphysics approach for magnetotail reconnection.
From [1]
Oversimplified sketch of a multiphysics approach for magnetotail reconnection.
From [1]
Framework Description and Performance
The muphyII framework, written in C++, base provides communication and the logistics of interface coupling for block-based domain decomposition on cartesian grids. Within each regional block resides a corresponding plasma solver that manages the algorithmic and numeric intricacies. The core of each solver is written in Fortran90 to exploit the conceptual simplicity of Fortran arithmetics. On top of that, MPI is used for distributed memory parallelization, and OpenACC for shared memory parallelization. The plasma solvers are stencil-based and require only elementary vector operations, an optimal case for OpenACC deployment on GPUs.The software has been designed around instances of Block, an object assigned to each subregion of the domain on a rectangular grid, which is associated with a specific MPI process. The numeric details of each plasma model are implemented in a Model object, and the algorithmic subtleties of combining models are handled by Scheme objects, which also provide interface boundary data exchange routines. Each Block holds the respective scheme for the plasma solver assigned to that region.
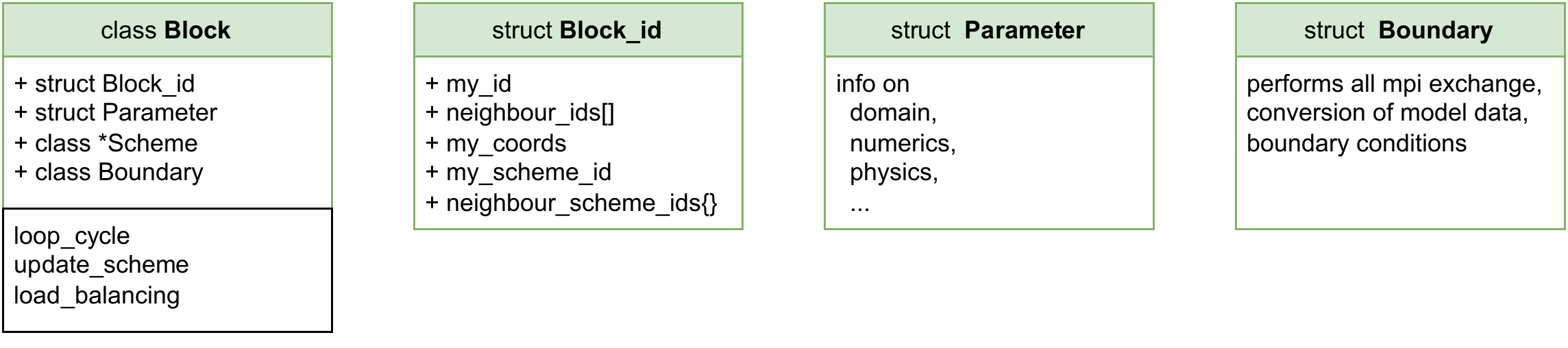 The framework of muphyII, which is responsible for the parallelization, boundary exchanges and conversions, data output, and scheme/model adaption, is mostly hidden from the user.
From [2]
The framework of muphyII, which is responsible for the parallelization, boundary exchanges and conversions, data output, and scheme/model adaption, is mostly hidden from the user.
From [2]
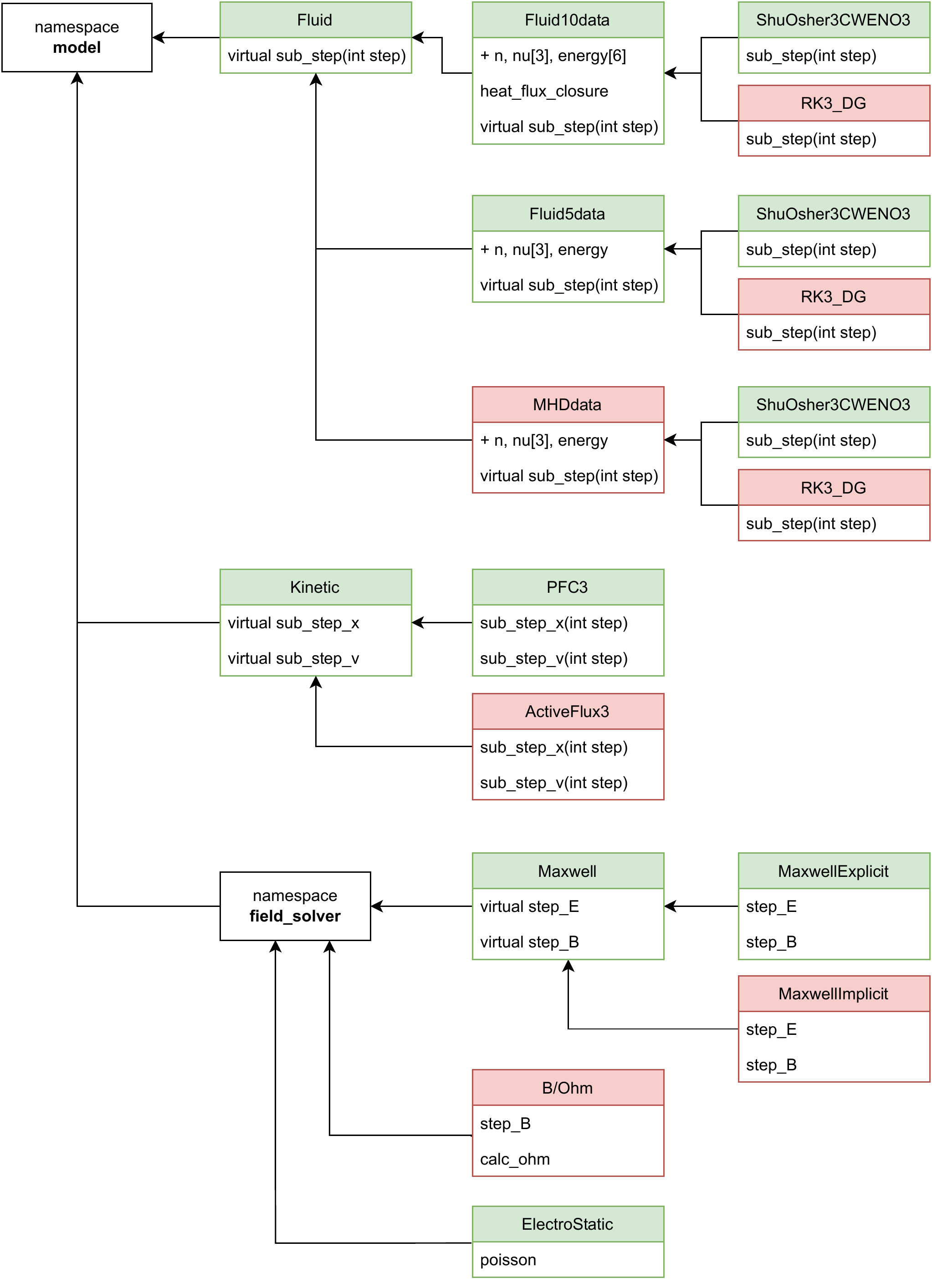 The class Scheme contains all possible combinations of the Model classes. Models colored green are stable, whereas the models colored red are work in progress.
From [2]
The class Scheme contains all possible combinations of the Model classes. Models colored green are stable, whereas the models colored red are work in progress.
From [2]
Functionalities
muphyII currently implements kinetic Vlasov-Maxwell, fluid 10-moment-Maxwell and fluid 5-moment-Maxwell models and provides up to five model combinations. These can be used standalone, statically coupled, or dynamically coupled. Here static coupling refers to prescribing a fixed model to each region, while dynamic coupling allows models to dynamically change in each region over the course of the simulation, based on predefined criteria that ideally identify the level of fidelity required in each spatial region [1], [3].
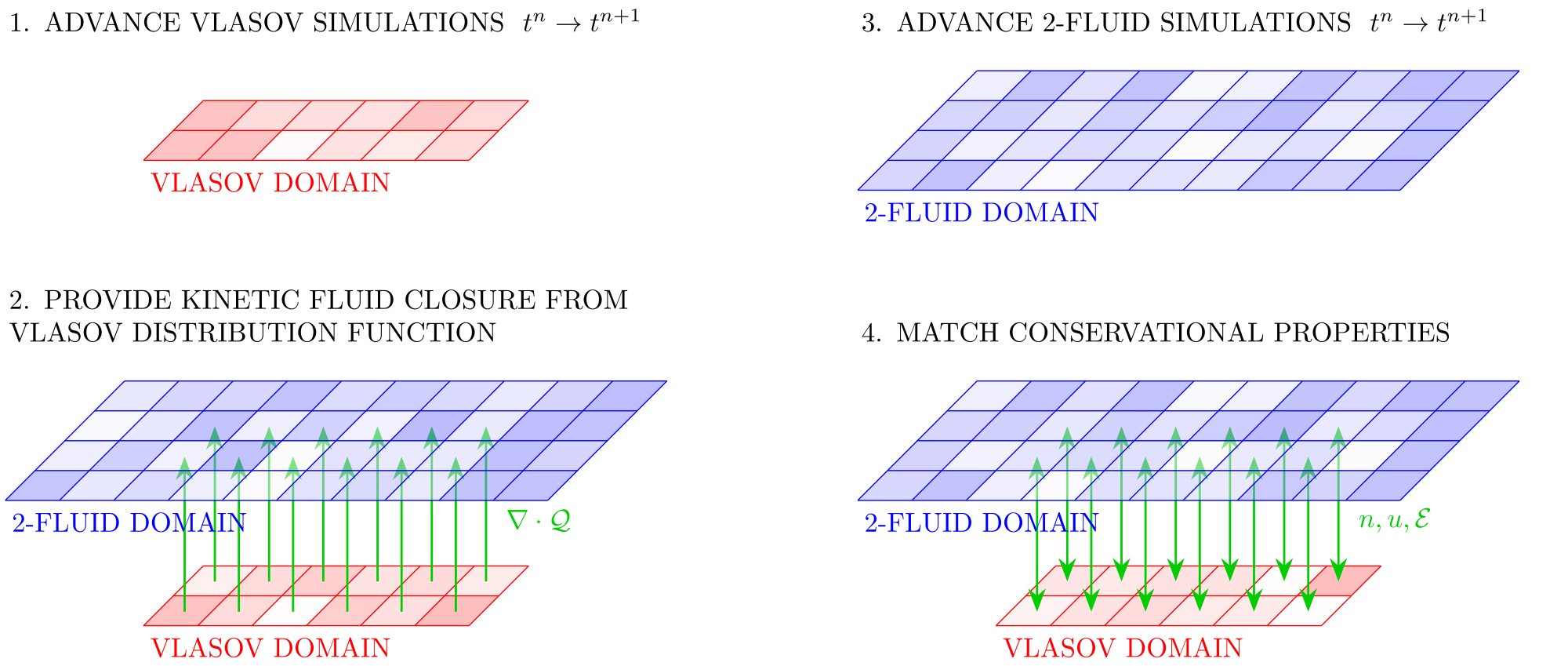
Energy-conserving Vlasov-Fluid coupling embedded into fluid region.
To account for differences of temporal scales in electron and ion physics, we employ electron subcycling, i.e. the time discretization for electons uses a smaller time step than for ions. [2]
Maxwell’s equations are solved on a Yee grid using the well-known finite difference time domain (FDTD) method. The fluid models use a finite volume discretization with the centrally weighted essentially non-oscillatory (CWENO) reconstruction [4] and Runge-Kutta (RK3) time integration [5] and perfectly conserve mass, momentum, and energy by design. Discontinuous Galerkin (DG) versions are in development. The Vlasov equation is solved with the third-order semi-Lagrangian positive flux-conservative (PFC) finite volume scheme [6] and conserves mass perfectly. Through advecting the Maxwellian part of the distribution function with a CWENO-RK3 scheme alongside the PFC Vlasov scheme, we can employ a maximum entropy moment-matching technique and nearly conserve momentum and energy as well [1]. A third-order Active Flux kinetic solver is soon to be integrated into the muphyII framework.
All user-side configuration, including initial and boundary conditions, is condensed to a single file that is evaluated at compile time. Templates are provided for common problems and benchmarks.
Outlook
muphyII has already been an invaluable help in the study of a number of different scenarios of magnetic reconnection and decying turbulence simulations [7], [8], [2]. We are currently working on extending the model hierarchy and include AMR magnetohydrodynamic (MHD) models in muphyII with asymptotic preserving MHD-fluid coupling. Further two-fluid descriptions like a 14-moment system [9] or a gyrotropic fluid model might be added in the future.
To truly utilize the separation of scales, we require adaptive mesh refinement (AMR). muphyII has been designed with AMR in mind to avoid conceptual problems later on, and AMR support is envisaged for the near future. Finally, the design of sophisticated criteria for adaptive model refinement is an open challenge.
References
- S. Lautenbach and R. Grauer, “Multiphysics simulations of collisionless plasmas,” Frontiers in Physics, vol. 6, 2018, doi: 10.3389/fphy.2018.00113.
- F. Allmann-Rahn, S. Lautenbach, M. Deisenhofer, and R. Grauer, “The muphyII code: Multiphysics plasma simulation on large HPC systems,” Computer Physics Communications, vol. 296, 2024, doi: 10.1016/j.cpc.2023.109064.
- S. Lautenbach, “Hierarchical multiphysics simulations of collisionless plasmas,” PhD Thesis, 2021.
- A. Kurganov and D. Levy, “A Third-Order Semidiscrete Central Scheme for Conservation Laws and Convection-Diffusion Equations,” SIAM Journal on Scientific Computing, vol. 22, no. 4, pp. 1461–1488, Jan. 2000, doi: 10.1137/S1064827599360236.
- C.-W. Shu and S. Osher, “Efficient implementation of essentially non-oscillatory shock-capturing schemes,” Journal of Computational Physics, vol. 77, no. 2, pp. 439–471, Aug. 1988, doi: 10.1016/0021-9991(88)90177-5.
- F. Filbet, E. Sonnendrücker, and P. Bertrand, “Conservative Numerical Schemes for the Vlasov Equation,” Journal of Computational Physics, vol. 172, no. 1, pp. 166–187, Sep. 2001, doi: 10.1006/jcph.2001.6818.
- F. Allmann-Rahn, S. Lautenbach, R. Grauer, and R. D. Sydora, “Fluid simulations of three-dimensional reconnection that capture the lower-hybrid drift instability,” Journal of Plasma Physics, vol. 87, no. 1, 2021, doi: 10.1017/S0022377820001683.
- F. Allmann-Rahn, S. Lautenbach, and R. Grauer, “An energy conserving Vlasov solver that tolerates coarse velocity space resolutions: Simulation of MMS reconnection events,” Journal of Geophysical Research: Space Physics, vol. 127, no. 2, 2022, doi: 10.1029/2021JA029976.
- J. McDonald and M. Torrilhon, “Affordable robust moment closures for CFD based on the maximum-entropy hierarchy,” Journal of Computational Physics, vol. 251, pp. 500–523, Oct. 2013, doi: 10.1016/j.jcp.2013.05.046.